Knowledge Problems

Tuesday, April 11, 2006

The Lay of the Land




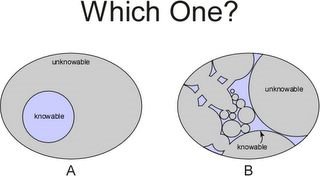
How can we ever know which of the above landscapes describes the relation between the physical world and our capacity to know that world? Does this matter in any practical sense? I suspect it does, because just as the topology of an error surface affects the convergence properties of optimization algorithms, the topology of the "knowledge surface" should affect the convergence properties of knowledge acquisition algorithms, i.e., science. Thus, we must find out what the landscape really looks like, but how?

posted by Big-S Skeptic at Tuesday, April 11, 2006

6 Comments:

  • Hmmm, you clearly know something about topology. Which is a good deal more than I know. I did not intend the drawing to represent a formal set-theoretic notion. It's just an informal suggestion that the asymptotic match between "the external world" and the "the world as described by a particular Knowledge Representation scheme" may have characteristics highly undesirable for inductive learning.

    By Blogger Big-S Skeptic, at Apr 23, 2006, 2:12:00 AM  

  • So your point was just that my post was confusing? I will try to clarify the issues in some future posts.

    By Blogger Big-S Skeptic, at Apr 23, 2006, 11:50:00 AM  

  • Good question.

    However it may be better to illustrate in a multi-dimensional way, becuase we understand things on many different levels.

    Also each person processes information differently, so if we be both "know" the same thing we still don't know it the same way.

    By Anonymous Anonymous, at Jun 1, 2006, 11:10:00 AM  

  • Interesting observations, Deep Thinker. I agree on both counts.

    By Blogger Big-S Skeptic, at Jun 5, 2006, 10:10:00 AM  

  • I understand the dilemma presented here completely. Very well put. The answer, I think, is that we can't know what the topology is. One way to guess would be to enter the knowable space from different angles at different starting points and see if the two points fail to converge. Practically I'm not sure how you would do this. Totally a huge fan of your blog so far. I did a google search for "hierarchy of knowledge claims knowable unknowable meaningful" hoping to find something exactly like your blog. I'm looking forward to your next posts.

    By Blogger Robert, at Jun 11, 2009, 4:55:00 PM  

  • Thanks so much Robert. I'm glad you enjoyed it. I've been taking a bit of a hiatus, as you can see from the posting dates. Perhaps I will resume again in the next few months. Good luck with your continuing search for understanding! --Big

    By Blogger Big-S Skeptic, at Jun 14, 2009, 8:29:00 AM  

Post a Comment

<< Home